KMP(Knuth-Morris-Pratt)算法是一种高效的字符串匹配算法,由Donald Knuth、Vaughan Pratt和James H. Morris三人于1977年联合发表,它的主要优点是在文本串中查找一个模式串时,具有线性的时间复杂度,即O(n+m),其中n为文本串的长度,m为模式串的长度,这使得KMP算法在实际应用中具有很高的效率,尤其是在处理大规模文本数据时。
KMP算法的核心思想是利用已知的部分匹配信息,避免在文本串中的每个字符上都进行完全的匹配检查,为了实现这一目标,KMP算法引入了一个名为“部分匹配表”的数据结构,用于存储模式串中每个子串的最长公共前后缀长度,通过这个表,KMP算法可以在匹配过程中跳过一些不必要的字符比较,从而提高匹配速度。
KMP算法的具体步骤如下:
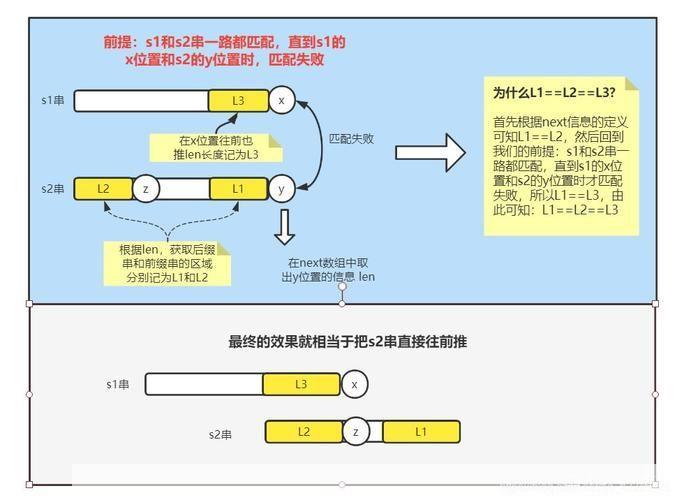
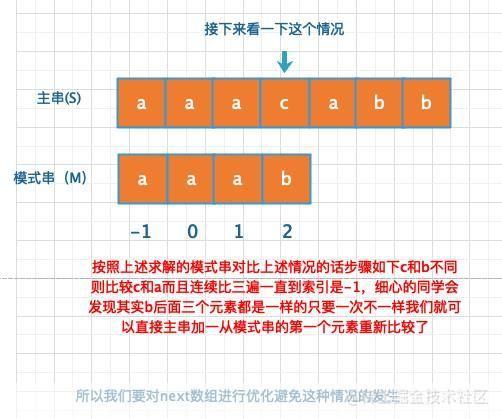
1、构建部分匹配表:从模式串的第一个字符开始,依次计算每个子串的最长公共前后缀长度,并将结果存储在部分匹配表中,具体来说,对于模式串的第i个字符,其最长公共前后缀长度等于其前面的j个字符(0≤j<i)与前面的j个字符组成的子串的最长公共前后缀长度,当j=0时,最长公共前后缀长度为0;当j>0时,最长公共前后缀长度等于当前字符与前面的j-1个字符组成的子串的最长公共前后缀长度加上前面的j-1个字符与前面的j-1个字符组成的子串的最长公共前后缀长度。
2、匹配过程:在文本串中从第一个字符开始,依次与模式串进行比较,如果在某个位置上,文本串的当前字符与模式串的当前字符相等,则继续比较下一个字符;否则,根据部分匹配表跳过一些不必要的字符比较,具体来说,对于模式串的第i个字符,如果在文本串中找到了与其相等的字符,则继续比较下一个字符;如果没有找到相等的字符,则根据部分匹配表跳过一些不必要的字符比较。
3、重复步骤2,直到模式串的所有字符都被匹配完或者遇到不匹配的情况。
KMP算法的应用非常广泛,可以用于字符串搜索、文本编辑器中的查找替换功能、编译器中的词法分析等场景,KMP算法还可以与其他字符串匹配算法(如Boyer-Moore算法、Sunday算法等)结合使用,以提高整体的匹配效率。